SIGGRAPH 2022

DeltaConv: Anisotropic Operators for Geometric Deep Learning on Point Clouds

Ruben Wiersma¹, Ahmad Nasikun^{1, 2}, Elmar Eisemann¹, and Klaus Hildebrandt¹
¹Delft University of Technology, ²Universitas Gadjah Mada

Code Paper PDF Supplement PDF Cite Replicability Stamp

Abstract

Learning from 3D point-cloud data has rapidly gained momentum, motivated by the success of deep learning on images and the increased availability of 3D data. In this paper, we aim to construct anisotropic convolution layers that work directly on the surface derived from a point cloud. This is challenging because of the lack of a global coordinate system for tangential directions on surfaces. We introduce DeltaConv, a convolution layer that combines geometric operators from vector calculus to enable the construction of anisotropic filters on point clouds. Because these operators are defined on scalar- and vector-fields, we separate the network into a scalar- and a vector-stream, which are connected by the operators. The vector stream enables the network to explicitly represent, evaluate, and process directional information. Our convolutions are robust and simple to implement and match or improve on state-of-the-art approaches on several benchmarks, while also speeding up training and inference.

Summary

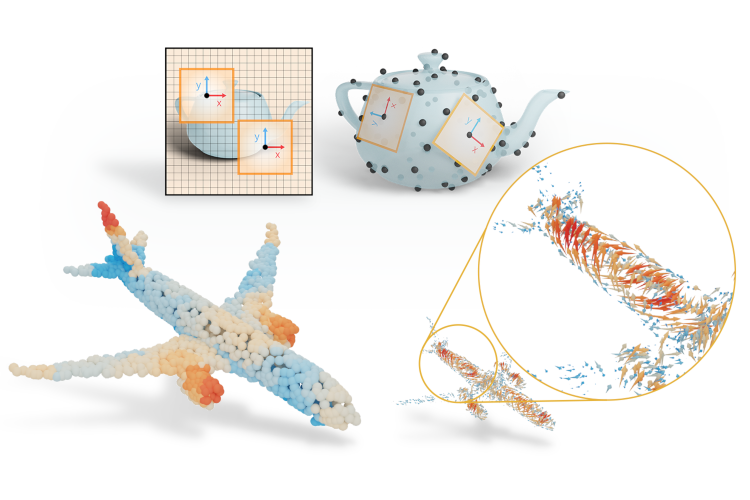
Anisotropic convolution is a central building block of CNNs but challenging to transfer to surfaces: Consider a CNN on images. Because an image has a globally consistent up-direction, the network can build anisotropic filters that activate the same way across the image.

Because we do not have a global coordinate system on surfaces, one cannot build and use anisotropic filters in the same way as on images. This limits current intrinsic convolutions on point clouds.

DeltaConv

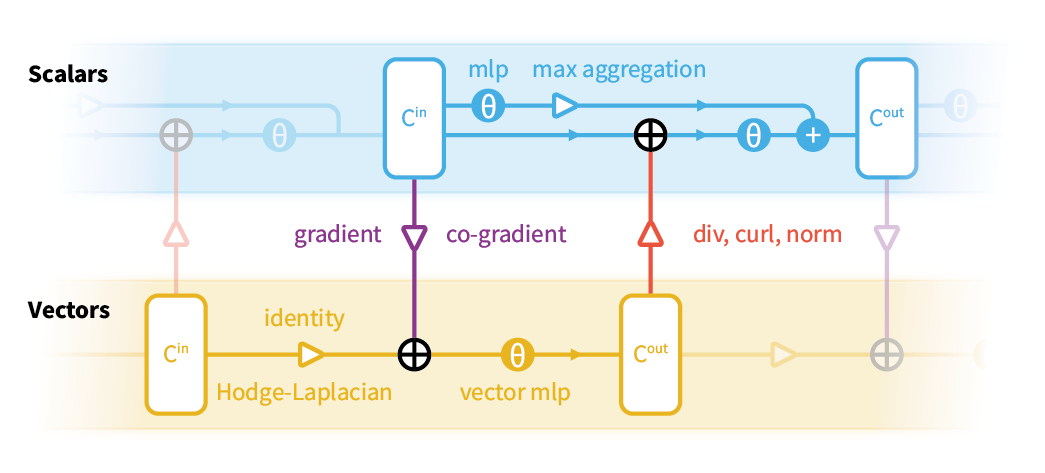
DeltaConv is described in terms of geometric operators instead of kernels. A well known operator that has been used widely in geometric deep learning is the Laplacian. While the Laplacian is a natural fit for intrinsic learning on surfaces, it is isotropic.

A classical way of creating anisotropic operators is to write the Laplacian as the divergence of the gradient and apply a linear or non-linear operation on the intermediate vector field. DeltaConv builds on this idea by constructing learnable anisotropic operators from elemental geometric operators: the gradient, co-gradient, divergence, curl, Laplacian, and Hodge-Laplacian. Because the operators output scalars and vectors, DeltaConv splits into a scalar- and vector stream.

DeltaConv is anisotropic The building blocks of DeltaConv allow it to construct anisotropic operators. A simple architecture with only a few DeltaConv blocks demonstrates state-of-the-art performance on several benchmarks.
DeltaConv is easy to implement You only need two sparse matrices that represent gradient and divergence. Everything else can be implemented with matrix multiplication and standard MLPs. Our implementation is available on github and you can install it with pip: pip install deltaconv.
DeltaConv generalizes across representations We implemented DeltaConv for point clouds and images, but the building blocks generalize to other representations. For example, an implementation for meshes could use finite element discretizations or discrete exterior calculus.
DeltaConv is coordinate-independent Because each geometric operator is coordinate-independent, the network as a whole is independent to local choices of coordinate systems.
DeltaConv is isometry invariant DeltaConv inherits orientation-preserving isometry-invariance from the geometric operators. It’s simple to make DeltaConv invariant to orientation flips as well: simply remove the co-gradient and curl operators.

The result is an intrinsic and anisotropic convolution layer that can be used in typical neural architectures for learning on point clouds.

Results

DeltaConv achieves state-of-the-art results in a simple architecture: 93.8% accuracy on ModelNet40, 86.9mIoU on ShapeNet, and 84.7% accuracy on the most difficult variant of ScanObjectNN. Meanwhile, it’s faster than previous edge-based convolutions, because it represents directional features at points instead of edges.

A simple example on images illustrates the difference with other convolution layers for point clouds. We apply a classical anisotropic diffusion operator (Perona-Malik) on images and overfit a ResNet with different convolution layers on the result. DeltaConv is able to approximate the anisotropic diffusion process and is also able to mimic different diffusion times, where other convolutions struggle.

Courtesy NASA.

Learn more

Find out more about DeltaConv in our paper, or come see our (virtual) presentation at SIGGRAPH 2022.

Code Paper PDF Supplement PDF Cite Replicability Stamp

Contact

r.t.wiersma [at] tudelft.nl, k.a.hildebrandt [at] tudelft.nl

Computer Graphics and Visualization group TU Delft

Cite

@Article{Wiersma2022DeltaConv,
  author    = {Ruben Wiersma, Ahmad Nasikun, Elmar Eisemann, Klaus Hildebrandt},
  journal   = {Transactions on Graphics},
  title     = {DeltaConv: Anisotropic Operators for Geometric Deep Learning on Point Clouds},
  year      = {2022},
  month     = jul,
  number    = {4},
  volume    = {41},
  doi       = {10.1145/3528223.3530166},
  publisher = {ACM},
}